La théorie cinétique du gaz parfait

---

1. Du macroscopique au microscopique

D'un point de vue macroscopique l'état gazeux est décrit par une équation d'état appelée loi du gaz parfait: p.V= n.R.T

• p : pression (Pa),

• V : volume occupé (m³),

• R: constante des gaz (8,31 J.K^-1.mol^-1),

• n : quantité de matière (mol),

• T : température absolue (K),

Au niveau microscopique, un modèle du comportement des molécules de gaz a été imaginé grâce à la théorie cinétique dont les hypothèses sont les suivantes :

• Les dimensions des molécules sont négligeables par rapport aux distances intermoléculaires. Le covolume (volume propre des molécules) est négligeable par rapport au volume occupé par le gaz. Pour le gaz parfait, il est nul.

• Les interactions intermoléculaires sont infiniment faibles voire nulles,

• Les molécules se déplacent en ligne droite. Si elles entrent en collision avec les parois du récipient ou avec d'autres particules, ces chocs sont parfaitement élastiques (conservation de la quantité de mouvement et de l'énergie cinétique).

Toutes ces conditions ne sont remplies que pour le gaz parfait. Elles sont néanmoins acceptables pour les gaz réels sous faible pression et à haute température.

Dans ce modèle, la pression du gaz résulte du nombre de collisions par unité de temps et de surface contre les parois du récipient. Par ailleurs, les chocs entre molécules modifient en permanence leurs vitesses. Toutefois, à un instant donné, à une température définie et pour un type de particule, la répartition statistique des vitesses ne varie pas.
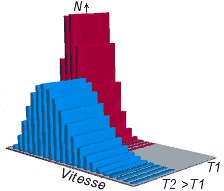
La distribution des vitesses obéit à la relation de Maxwell-Boltzmann :

N(v)=4πv².(m/2πkT)^3/2.exp(-mv²/2kT).

La théorie cinétique nous apprend que l'énergie cinétique moyenne d'une mole de gaz est proportionnelle à la température, Ec = 3/2 RT.
On confirme ainsi que la vitesse quadratique moyenne d'une molécule est bien une fonction de la température, v* = (3kT/m)^1/2 (k = constante de Boltzmann).
Quant à la vitesse moyenne, son expression est: v = (8kT/πm)^1/2.

Cette dernière relation nous permet de constater qu'à une même température, les molécules de gaz lourds sont plus lentes.

 

2. Relation entre la pression et le nombre de collisions

Au premier abord, on pourrait s'imaginer que la pression est directement proportionnelle au nombre de chocs par unité de temps contre les parois. Comme nous allons le démontrer, c'est une affirmation hasardeuse ...

Envisageons un gaz emprisonné dans un récipient cubique de volume d³. Intéressons-nous à une molécule voyageant par exemple parallèlement à l'axe ox. Cette molécule, animée d'une vitesse v, entre en collision avec une face du cube v / 2d fois par unité de temps. En effet entre deux chocs, elle doit parcourir l'aller et le retour soit deux fois le côté du cube.

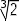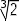Considérons maintenant un autre cube dont le volume vaut la moitié du précédent, d³/2, la longueur de son côté est d /. Une molécule, animée d'une vitesse v en mouvement parallèle à ox, entre en collision avec une face du cube v / 2d / fois par unité de temps. Pour les deux cas, le rapport des nombres de collisions par unité de temps vaut donc!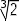

Dès lors comment expliquer que la pression double lorsque le volume diminue de moitié ?

En réalité, comme l'expression de la pression correspond au quotient de la force à la surface sur laquelle elle s'exerce, il faut évaluer le nombre de collisions par seconde et par unité de surface.

Dans le premier cas le nombre de collisions par unité de temps et par unité de surface est égal à v / 2d³. Dans le second cas ce nombre vaut v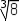/ 2d³ ou encore v / d³.

Pour un volume réduit de moitié, le nombre de collisions par unité de temps et par unité de surface double, ce qui a pour effet de multiplier par deux également la pression.